Transformations and Associations

In the project you will need to correctly perform observation measurement transformations, along with identifying measurement landmark associations in order to correctly calculate each particle's weight. Remember, our ultimate goal is to find a weight parameter for each particle that represents how well that particle fits to being in the same location as the actual car.

In the quizzes that follow we will be given a single particle with its position and heading along with the car's observation measurements. We will first need to transform the car's measurements from its local car coordinate system to the map's coordinate system. Next, each measurement will need to be associated with a landmark identifier , for this part we will take the closest landmark to each transformed observation. Finally, we will use this information to calculate the weight value of the particle.

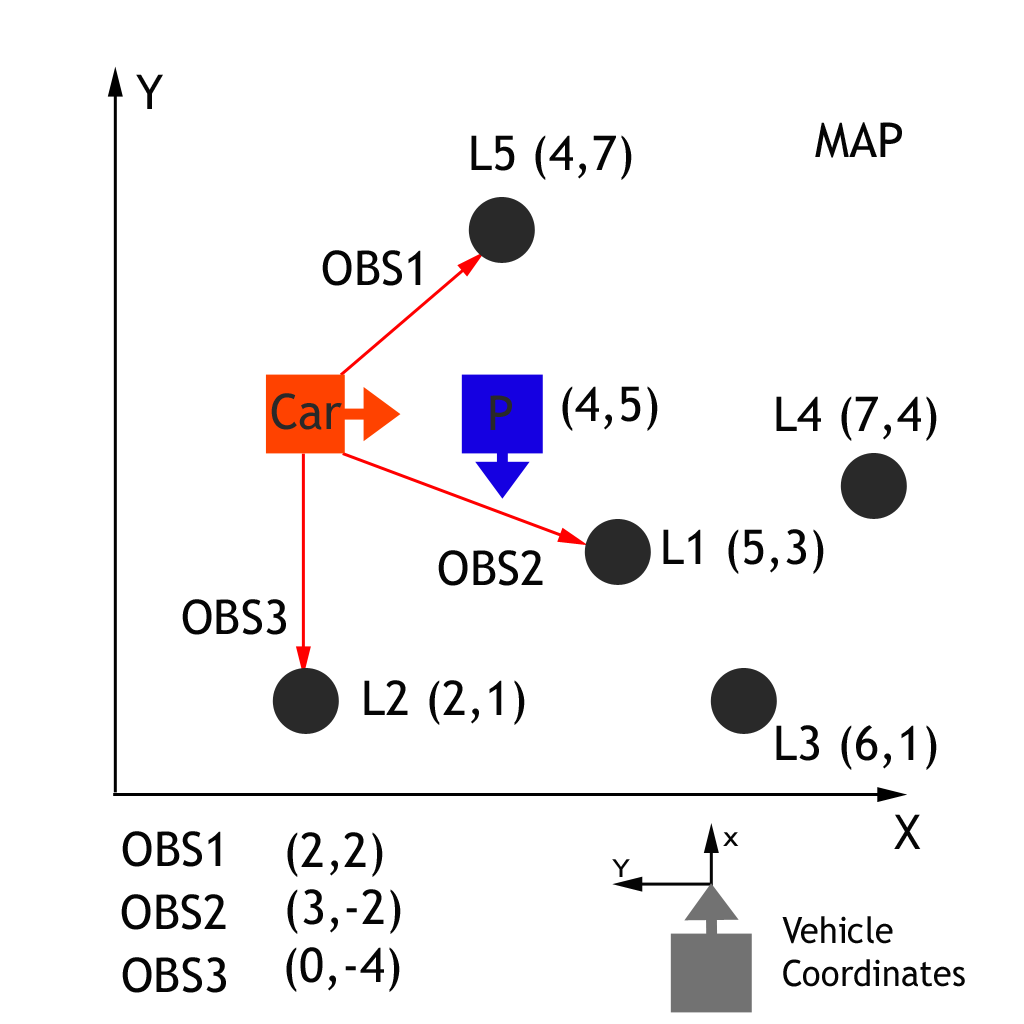
In the graph above we have a car ( ground truth position ) that observes three nearby landmarks, each one labeled OBS1, OBS2, OBS3. Each observation measurement has x, and y values in the car's coordinate system. We have a particle "P" ( estimated position of the car ) above with position (4,5) on the map with heading -90 degrees. The first task is to transform each observation marker from the vehicle's coordinates to the map's coordinates, with respect to our particle.